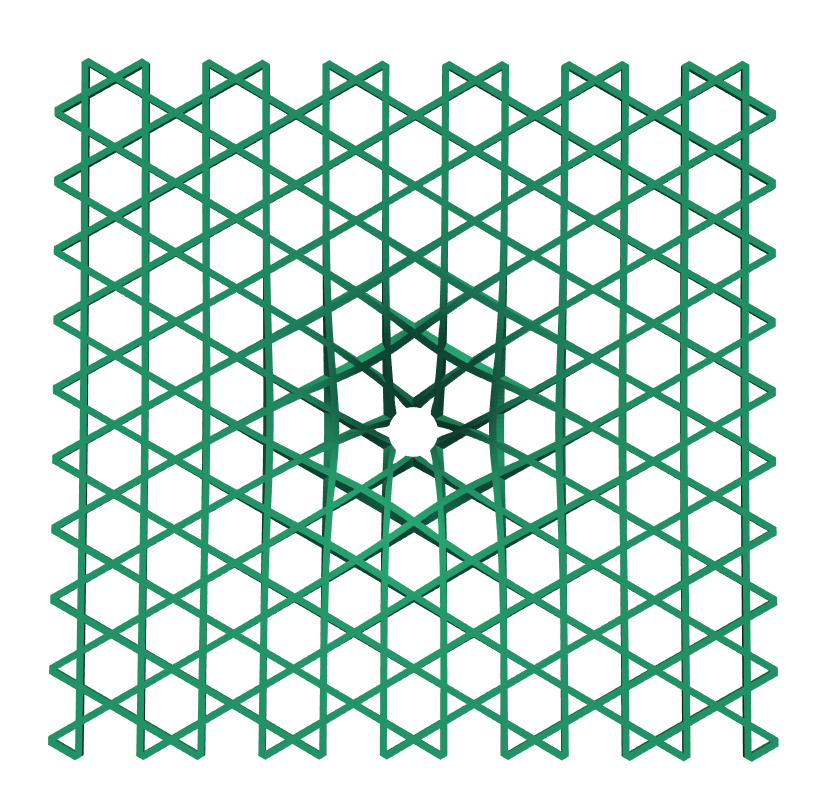
Create building with Kagome pattern

In this example, we demonstrate how HelloTriangle can support the design of advanced architectural structures—specifically by generating a building with the Kagome pattern, a well-known geometric motif..

This example highlights the power of symmetry in script-based modeling. At first glance, the Kagome pattern appears as a web of triangles, but when we break it down, each triangle is formed from three symmetrical sides, and each side is made of two mirrored halves. To check this, we recommend to visualize the intermediate meshes used in the script.

To transform the 2D pattern into a dynamic 3D structure, we modify the Z-coordinates using the arctan function from NumPy, creating a warped surface. Finally, we give the beams real-world thickness by offsetting the 2D triangle elements, turning them into solid 3D prism elements.

Whether you're exploring parametric design or generative architecture, this example shows how using code makes it easy to create complex 3D designs from simple building blocks. The Kagome pattern is a great example of how symmetry and a few lines of Python can turn a flat pattern into an interesting 3D structure.

from hellotriangle import shapes
import numpy as np

# dimensions
l = 1.0 # edge length of basic triangle
w = 0.2 # width
t = 0.3 # thickness

# mesh parameters
ne = 3  # number of elements along half of a basic edge

# height of the basic triangle
h = l*np.sqrt(3.0)/2.0

# create basic unit
centerline = shapes.line([0.0, 0.0, 0.0], [l/2.0, 0.0, 0.0], n = ne)
outerline = shapes.line([0.0, w/2.0, 0.0], [l/2.0 - w/(2*np.tan(60.0/180.0*np.pi)), w/2.0, 0.0], n = ne)
innerline = shapes.line([0.0, -w/2.0, 0.0], [l/2.0 - w/(2*np.tan(30.0/180.0*np.pi)), -w/2.0, 0.0], n = ne)

part1 = centerline.connect(outerline)
part2 = centerline.connect(innerline)

unit = part1 + part2

# create basic triangular shape
unit = unit.translate([0.0, h/3.0, 0.0])
unit2 = unit.reflect(dir = 0)
triangle = (unit + unit2).rosette(3).translate([0.0, -h/3.0, 0.0])

# 2nd rotated basic triangular shape
triangle2 = triangle.rotate_Z(180.0)
triangle2 = triangle2.translate([l, 0.0, 0.0])
triangles = (triangle + triangle2).translate([0.0, 0.0, 0.0])

# replicate basic triangles
row1 = triangles.replicate(n = 10, step = 2*l)
row2 = row1.reflect(dir = 1).translate([0.0, -2*h, 0.0])
full = (row1 + row2).replicate(n = 6, dir = [0.0, 1.0, 0.0], step = 4*h)

# center
full = full.translate([-10*l, -9*h, 0.0])

# add function to Z coordinates
X = full.coords.x
Y = full.coords.y

R = np.sqrt(X**2 + Y**2)
full.coords.z = np.arctan(R-l)*5.0

# cut
fullCut = full.convert('tri3').cutWithPlane([0.,0.,0.5],[0.,0.,1.], side='+')

# offset 
outer = fullCut.offset(distance=t)

# create prism elements, by connecting inner and outer triangle mesh
prism = fullCut.connect(outer, div=1)

# draw
draw(prism, color = "#2BB786")

Figure: Building with Kagome pattern (view 1)

Figure: Building with Kagome pattern (view 2)

Figure: Building with Kagome pattern (view 3)